BF16 vs FP16 for Reinforcement Learning: Where Are We?
Deep Dives
Explore related topics with these Wikipedia articles, rewritten for enjoyable reading:
-
Floating-point arithmetic
7 min read
The article's core topic is the difference between BF16 and FP16 precision formats. Understanding how floating-point representation works—mantissa bits, exponent ranges, and rounding errors—is essential context for grasping why these format choices matter for machine learning stability.
-
Reinforcement learning from human feedback
13 min read
The article discusses GRPO, GSPO, and RL training methods for language models. RLHF is the foundational technique that these algorithms build upon, and understanding it provides crucial context for why training stability and reward collapse are such significant concerns.
-
Numerical stability
11 min read
The central problem discussed—rounding errors compounding over sequence length and causing training divergence—is fundamentally about numerical stability in algorithms. This mathematical concept explains why small precision differences can cascade into catastrophic failures.
Hi Everyone,
In this edition of The Weekly Kaitchup, I discuss the current state of the BF16 vs FP16 debate for RL and MiniMax-M2’s “Interleaved Thinking”.
Book Update
If you’ve already purchased the book, the next update will land in your inbox on Monday. This release includes:
A full review of all chapters
Refreshed notebooks
A new section on NVFP4 quantization
A short chapter on efficient inference with vLLM
Everything is now bundled into a single 140-page PDF plus 9 companion notebooks.
One chapter is still in progress: LLM Evaluation. It’s one of the most important topics of the book. I’ll publish this chapter in December.
You can still grab the book at 30% off until November 30.
At NeurIPS
I’ll be at NeurIPS in San Diego, December 3–6. If you’re around, let’s meet up!
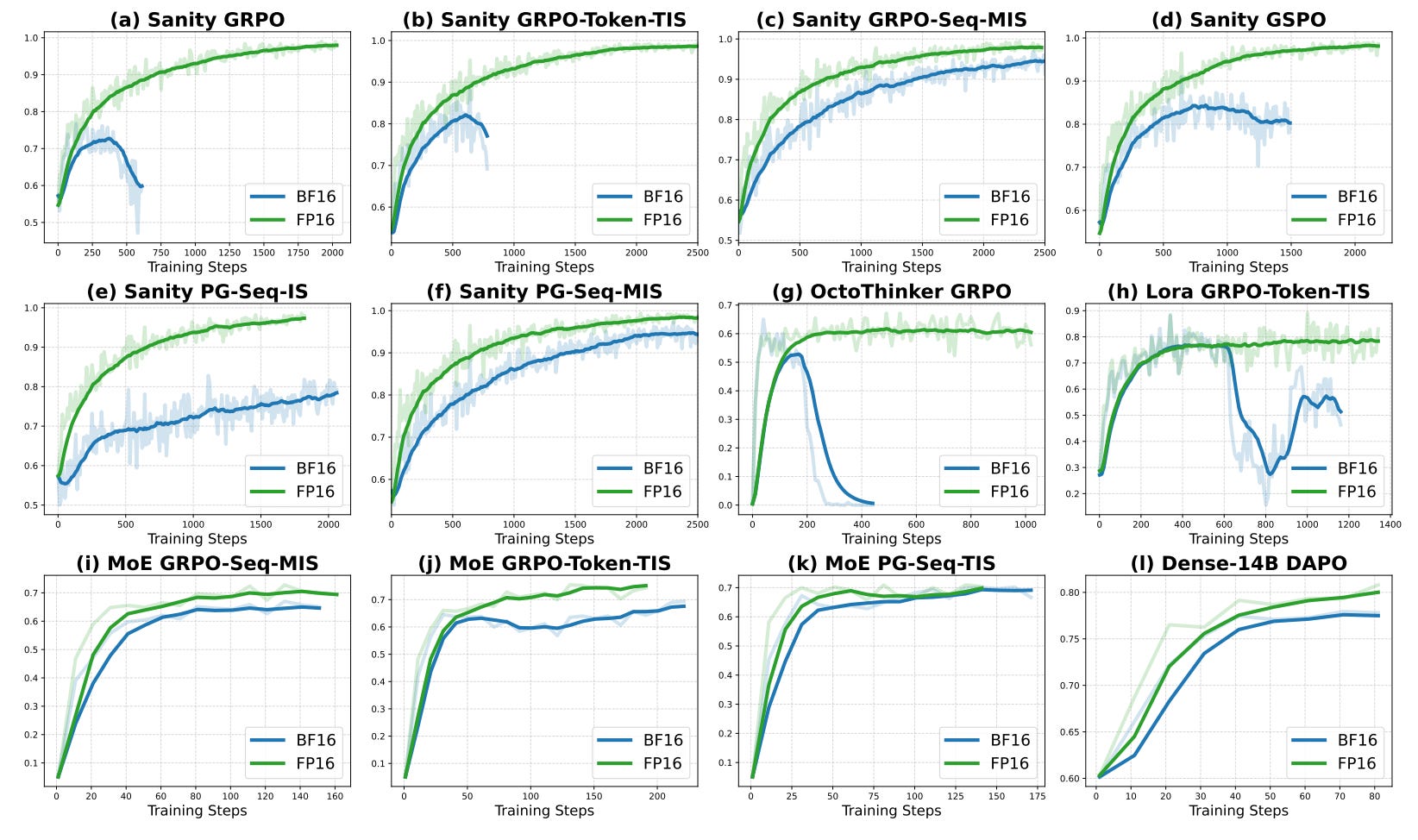
A recent arXiv paper, “Defeating the Training-Inference Mismatch via FP16” (October 31, 2025), argues that BF16’s lower mantissa precision introduces small rounding errors during autoregressive generation, which can have a large impact during RL.
Because rollouts and training often run on different engines, for example vLLM for inference and PyTorch FSDP for training, those BF16 rounding differences cause the rollout policy to diverge from the training policy, biasing gradients, destabilizing learning with reward collapse, and creating a deployment gap. The proposed fix is to switch to FP16, which has more mantissa bits and reduces rounding error, stabilizing training without algorithmic changes.
Though surprising, community experiments largely corroborate the claim.
In detail, the authors trained on NVIDIA A100s using VeRL, Oat, DeepSpeed, and vLLM across GRPO and GSPO.
They attribute the training-inference mismatch to BF16 rounding differences between engines that compound with sequence length, biasing importance sampling ratios and encouraging divergence. Offline analyses report roughly 7.64 token-level KL for BF16 versus 0.32 for FP16, about a 24x reduction, and the mismatch grows with length.
On a sanity set of 1,460 MATH problems where perfect accuracy is reachable and on AIME 2024, BF16 often collapses between about 150 and 600 steps, while FP16 trains stably to near-perfect accuracy without corrective tricks.
BF16 tends to peak early and then diverge. FP16 is typically 1.5 to 2x faster to convergence. Using FP32 inference on top of BF16 training can stabilize results but at roughly three times the compute. The advantage appears tied to lower variance in likelihood ratios and the roughly 24x lower KL with FP16.
Note:
...This excerpt is provided for preview purposes. Full article content is available on the original publication.