Tiny Recursive Models for Very Specific Problems

Hi Everyone,

In this edition of The Weekly Kaitchup:

• “LoRA without Regret” and Rank=1

• Granite 4.0 in The Kaitchup Index

• Tiny Recursive Models for Very Specific Problems

“LoRA without Regret” and Rank=1

One of the most surprising takeaways from the Thinking Machines article we covered in last week’s Weekly Kaitchup is that GRPO-style reinforcement learning with a LoRA rank of 1 can match the performance of full GRPO (i.e., updating all weights). As expected, several people tried to validate this. Hugging Face shared a replication setup, and it seems to partially hold for their SmolLM 3 model:

LoRA Without Regret (by Hugging Face)

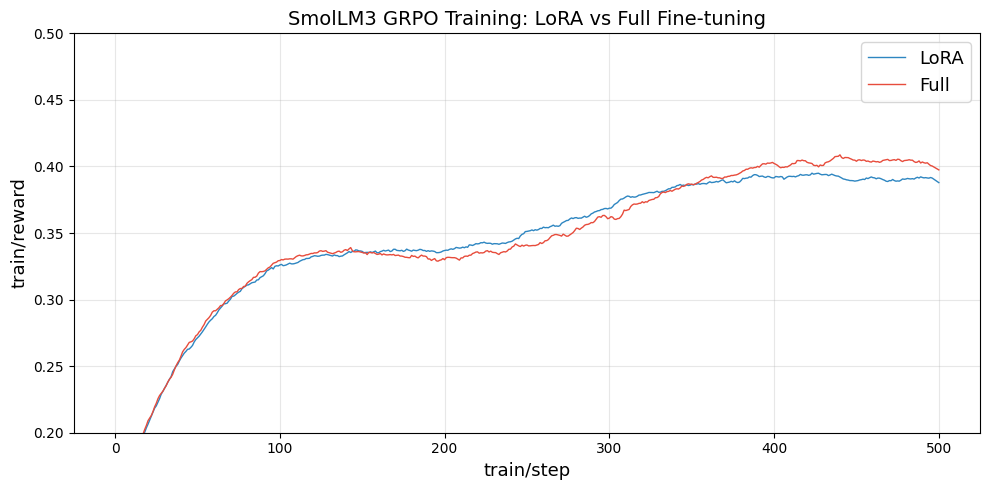
They got some good-looking learning curves confirming that LoRA with rank 1 is good:

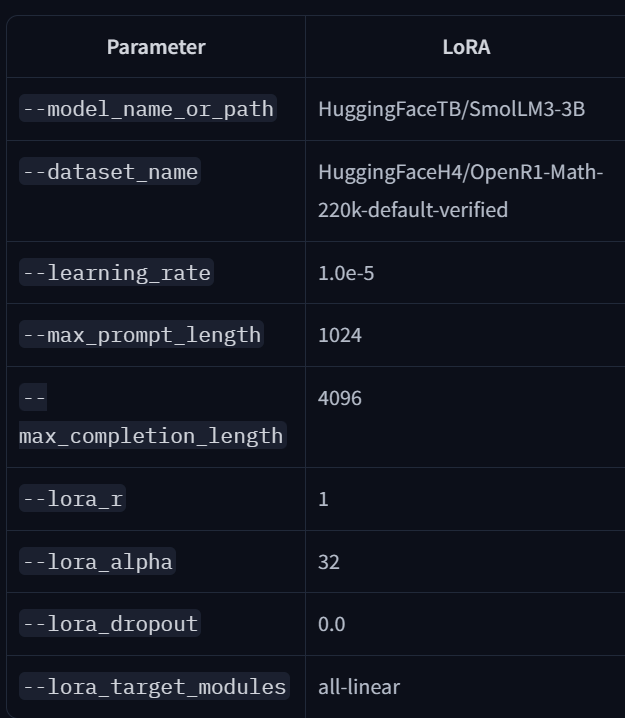
They used the following configurations applied to Qwen3-0.6B:

peft_config = LoraConfig(
    r=1,
    lora_alpha=32,
    target_modules=”all-linear”
)

training_args = GRPOConfig(
    learning_rate=5e-5,
    per_device_train_batch_size=1,
    gradient_accumulation_steps=4,
    num_train_epochs=1,
    num_generations=8,
    generation_batch_size=8,
    report_to=[”trackio”],
)

Early on, the curves overlap, LoRA (rank = 1) even leads briefly, but full fine-tuning pulls ahead and stays there. So rank-1 LoRA doesn’t behave identically to full training in practice. That doesn’t refute Thinking Machines’ claim that rank = 1 can be sufficient. Still, it suggests the training dynamics (optimizer, schedule, regularization, etc.) likely create a gap that keeps full training ahead, and it may not be trivial to close.
Let’s look at their hyperparameters:

These settings largely mirror Thinking Machines’. I’d be curious to see a domain beyond math: every successful rank-1 report I saw this week used math datasets. It’d be valuable to test other tasks, especially with datasets that were not generated by LLMs, or with noisier, harder-to-verify rewards.

Last week, I also ran rank-1 experiments using Unsloth’s new notebook to train GTP-OSS:

GRPO Training for GTP-OSS with Unsloth

Note: The notebook currently points to misnamed modules. As written, it only applies LoRA to self-attention and skips the expert layers. With rank = 1, that leaves ~500k trainable parameters, versus ~11.5M if all experts were correctly targeted.

The training objective in this notebook by Unsloth is quite original:

Our goal is to make a faster matrix multiplication kernel by doing RL on GTP-OSS 20B with Unsloth.

They define several reward functions for the task, worth reading in the notebook and trying yourself.

In my runs, I compared rank = 1 vs. rank = 64: the higher rank performed notably better. Rank-1 does learn (which is remarkable), but it didn’t reach the same reward